| (1) |
Возникновение этой научной дисциплины восходит к открытию рентгеновского излучения в 1895 году. В процессе опытов с рентгеновыми лучами А.Беккерель в 1896 году обнаружил радиоактивность. Изучение радиоактивности Резерфордом и его сотрудниками привело к ряду важных открытий, первым из которых было установление ядерной структуры атома. Возникшая в 10-е годы следующего века ядерная модель атома явилась основой для бурного прогресса ядерной физики и квантовой механики. Открытие в 1911-1912 гг. космических лучей явилось крупнейшим событием, оказавшим огромное влияние на последующие исследования физики микромира.
Свойства радиоактивности к этому времени были достаточно хорошо известны, но опыты с ионизацией воздуха позволяли предположить, что в дополнение к обычной радиоактивности действует излучение неизвестной природы с большой проникающей способностью. Были высказаны обоснованные предположения, что оно приходит из Космоса. Полеты на воздушных шарах, выполненные Гессом в 1911-1912 гг., подтвердили эту гипотезу и привели, таким образом, к открытию космического излучения.
В 30-е годы были обнаружены пучки частиц, одновременно проходящих на значительном удалении друг от друга.Первые такие следы были обнаружены в камере Вильсона, когда вполе зрения попадали одновременно треки нескольких частиц. Д.В.Скобельцын, обнаруживший эти явления в своих экспериментах, подсчитал,что частота событий много больше того, что могло бы наблюдаться чисто случайным образом. Дальнейшее изучение таких событий привело к представлению о каскадных процессах - "ливнях" частиц, возникающих в плотных средах, через которые проходят частицы космических лучей.
Картина каскадных процессов представляется сегодня следующей. Ядра в
составе космических лучей (протоны, альфа-частицы и ядра более тяжелых
элементов), сталкиваясь с ядрами вешества, порождают вторичные
частицы в реакциях:
| (1) |
Заряженные и нейтральные пионы примерно с таким же пробегом могут
взаимодействовать с нуклонами в ядрах вещества с порождением вторичных
частиц:
| (2) |
В промежутках между рождением и столкновением с нуклонами пионы
имеют вероятность распадаться по схеме:
| (3) |
Времена жизни до распала составляют для заряженных пионов - 2 10![]() с,
а для нейтральных - около 10
с,
а для нейтральных - около 10![]() с. Нужно иметь ввиду, что для частиц,
имеющих большие энергии, эти времена увеличиваются в
с. Нужно иметь ввиду, что для частиц,
имеющих большие энергии, эти времена увеличиваются в ![]() раз, где
раз, где
![]() - лоренц-фактор частицы.
- лоренц-фактор частицы.
Легко подсчитать, что заряженный пион даже не слишком большой энергии
(с лоренц-фактором не намного большим единицы) будет иметь пробег около
6 м и ,например, в воде почти никогда не будет распадаться из-за
преобладания столкновений. Однако, нейтральный пион в этой среде
будет, наоборот, почти всегда распадаться. Фотоны, возникающие при распадах
нейтральных пионов, порождают электронно-фотонный каскад посредством реакций
| (4) |
Первая из этих реакций называется фоторождением электрон-позитронных пар, а
вторая - тормозным излучением электронов. Обе эти реакции имеют примерно
одинаковое сечение (и соответственно пробег частиц до взаимодействия).
Реакции протекают в электрическом поле атомных ядер, поэтому они намного
интенсивнее идут в тяжелых веществах. Например, в свинце пробег до
взаимодействия составляет всего 7 г/см![]() , тогда как в воздухе он
равен 37 г/см
, тогда как в воздухе он
равен 37 г/см![]() . Электроны расходуют также энергию на ионизацию атомов
вещества. Эти потери составляют около 2 Мэ на каждый пройденный г/см
. Электроны расходуют также энергию на ионизацию атомов
вещества. Эти потери составляют около 2 Мэ на каждый пройденный г/см![]() .
Поэтому, если в процессе каскадного размножения энергия электронов
понизится до 80 МэВ, то они уже не будут дальше размножаться путем
тормозного излучения. Эта энергия называется критической энергией
электронов.
.
Поэтому, если в процессе каскадного размножения энергия электронов
понизится до 80 МэВ, то они уже не будут дальше размножаться путем
тормозного излучения. Эта энергия называется критической энергией
электронов.
Указанная совокупность каскадных процессов имеет место в любом веществе, в том числе и в воздухе. Ливни в воздухе обладают рядом особенностей. В разреженных слоях атмосферы на больших высотах, гле происходит подавляющая часть столкновений первичных частиц, значительная часть заряженных пионов распадается на мюоны, которые не являются ядерно-активными и поэтому достигают земной поверхности.
Очень важным обстоятельством является разлет вторичных частиц. Вторичные частицы сохраняют направление движения первичных частиц лишь приближенно. Дело в том, что всякий распад реальных или виртуальных частиц сопровождается появлением поперечного импульса и соответственно удаления частиц друг от друга в процессе их совместного движения. Разреженность атмосферы способствует удалению частиц ливня на расстояние порядка 100 м от оси - траектории, которую прочертила бы первичная частица в отсутствие столкновений. На периферии ливня редкие вторичные частицы могут удаляться от оси даже на расстояние одного километра. Если первичная энергия достаточно велика, то этих периферийных частиц достаточно много, чтобы зафиксировать приход ливня только по регистации этих частиц.
Ливни частиц в атмосфере были открыты случайно в процессе проверки электронных схем совпадений. Первые сведения о таких ливнях были сообщены французским физиком Пьером Оже в 1938 г. Современное название - широкие атмосферные ливни - подчеркивает их большую геометрическую протяженность.
Физическая картина широкого атмосферного ливня обусловлена небольшим числом элементарных процессов. Для того, чтобы воссоздать качественную картину пространственного развития, не претендующую на высокую точность, можно воспользоваться рядом упрощений.
Электронно-фотонный каскад представим как "расщепление" частиц надвое в поле
атомных ядер с образованием промежуточного состояния и его последующим
изотропным распадом. При этом нет необходимости различать сорта частиц.
Характерная длина, на которой этот процесс происходит, называемая каскадной
единицей, для воздуха составляет ![]() =37 г/см
=37 г/см![]() .
.
Из кинематики следует, что энергетический спектр продуктов при изотропном
распаде промежуточного состояния - как и любой быстро движущейся частицы -
имеет "плоский" вид:
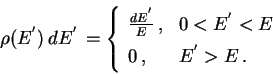 |
(5) |
Так как средняя энергия частиц в каждом акте взаимодействия уменьшается вдвое,
то с ростом числа каскадов ![]() логарифм энергии линейно убывает. Поэтому
удобно пользоваться средним логарифмом энергии, который в каждом каскаде
уменьшается на единицу. В самом деле,
логарифм энергии линейно убывает. Поэтому
удобно пользоваться средним логарифмом энергии, который в каждом каскаде
уменьшается на единицу. В самом деле,
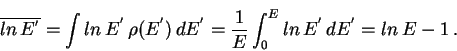 |
(6) |
| (7) |
| (8) |
Пространственное развитие электромагнитного ливня будем измерять глубиной
![]() , которая определяется в каскадных единицах. Распределение частиц,
рожденных в
, которая определяется в каскадных единицах. Распределение частиц,
рожденных в ![]() -м каскаде, по глубине
-м каскаде, по глубине ![]() дается формулой
дается формулой
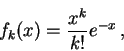 |
(9) |
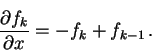 |
(10) |
Число частиц с энергией ![]() равно
равно ![]() . В действительности из-за
распределенного характера энергии следует говорить о числе частиц,
энергия которых превосходит указанное значение, и оно вполовину меньше:
. В действительности из-за
распределенного характера энергии следует говорить о числе частиц,
энергия которых превосходит указанное значение, и оно вполовину меньше:
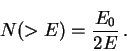 |
(11) |
Итак, число электронов на глубине ![]() с энергией большей, чем
с энергией большей, чем ![]() ,
выражается формулой:
,
выражается формулой:
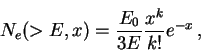 |
(12) |
 |
(13) |
Эта формула является каскадной кривой для нашего "модифицированного"
электромагнитного каскада. Максимум лавины, как видно из этого выражения,
достигается на глубине
| (14) |
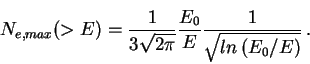 |
(15) |
Можно ожидать, что при большом числе каскадов (когда
![]() )
эта упрощенная теория будет давать удовлетворительную точность. Точная
(без учета ионизационных потерь) теория дает для числа электронов в
максимуме ливня следующее выражение (см., например, [1]):
)
эта упрощенная теория будет давать удовлетворительную точность. Точная
(без учета ионизационных потерь) теория дает для числа электронов в
максимуме ливня следующее выражение (см., например, [1]):
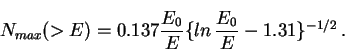 |
(16) |
Так как численный множитель в нашем выражении равен 0.133, то в указанном приближении больших логарифмов мы имеем, практически, полное совпадение с точной теорией, несмотря на сильные упрощения.
Ядерный каскад в упрощенном виде представляет собой множественное
рождение частиц, повторяемое многократно. Пробег до ядерного
взаимодействия примем равным
![]() , а множесвенность
рождения пионов
, а множесвенность
рождения пионов ![]() - постоянной. Хотя в реальном каскаде первичный протон
отдает не всю энергию в первом же взаимодействии, примем для упрощения,
что он порождает
- постоянной. Хотя в реальном каскаде первичный протон
отдает не всю энергию в первом же взаимодействии, примем для упрощения,
что он порождает ![]() частиц - пионов, - поровну распределяя между ними
энергию. Каждый нейтральный пион распадается на два гамма-кванта, а каждый
заряженный пион производит
частиц - пионов, - поровну распределяя между ними
энергию. Каждый нейтральный пион распадается на два гамма-кванта, а каждый
заряженный пион производит ![]() пионов следующего поколения. В силу
изотопической инвариантности число нейтральных пионов составляет 1/3
числа частиц, рожденных в каждом поколении.
пионов следующего поколения. В силу
изотопической инвариантности число нейтральных пионов составляет 1/3
числа частиц, рожденных в каждом поколении.
Так как энергия пионов ![]() -го поколения равна
-го поколения равна
| (17) |
| (18) |
| (19) |
Двойка появляется вследствие того, что учитывается распад нейтрального
пиона на два фотона. Подставляя ![]() , получим
, получим
| (20) |
| (21) |
| (22) |
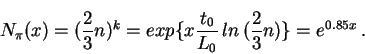 |
(23) |
Как только энергия пионов снизится до некоторого значения ![]() ,
включатся распады этих частиц и процесс размножения прекратится. Это
произойдет при
,
включатся распады этих частиц и процесс размножения прекратится. Это
произойдет при
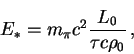 |
(24) |
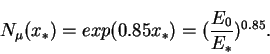 |
(25) |
Если определить число мюонов в диапазоне первичных энергий вблизи
10![]() эВ, то получим
эВ, то получим
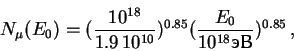 |
(26) |
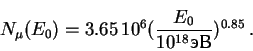 |
(27) |
Число электронов в ШАЛ на уровне моря определяется энергией, выделенной
в ![]() -мезоны. Хотя в каждом каскаде они уносят только 1/3
энергии, тем не менее, уже в верхних слоях атмосферы почти вся энергия
ливня переходит в электронно-фотонную компоненту. Поэтому число
электронов может быть оценено так, как если бы первичная частица была
фотоном. Критическая энергия, при которой ионизационные и радиационные
потери электронов сравниваются, составляет для воздуха примерно
-мезоны. Хотя в каждом каскаде они уносят только 1/3
энергии, тем не менее, уже в верхних слоях атмосферы почти вся энергия
ливня переходит в электронно-фотонную компоненту. Поэтому число
электронов может быть оценено так, как если бы первичная частица была
фотоном. Критическая энергия, при которой ионизационные и радиационные
потери электронов сравниваются, составляет для воздуха примерно
![]() = 80 МэВ и для полного числа электронов можем использовать
выведенную выше каскадную формулу, подставив туда критическую энергию:
= 80 МэВ и для полного числа электронов можем использовать
выведенную выше каскадную формулу, подставив туда критическую энергию:
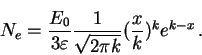 |
(28) |
Для ![]() эВ, например, получим
эВ, например, получим ![]() =23.2 и при
=23.2 и при ![]() =27 имеем
=27 имеем
| (29) |
Определим зависимость ![]() от энергии. Поскольку
от энергии. Поскольку ![]() зависит от величины
зависит от величины
![]() , которая является логарифмом первичной энергии, то зависимость
, которая является логарифмом первичной энергии, то зависимость ![]() от
энергии будет более крутой, чем линейная:
от
энергии будет более крутой, чем линейная:
| (30) |
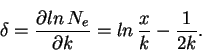 |
(31) |
 |
(32) |
Простые оценки показывают, что основной причиной, вызывающей отклонение мюонов
от оси ливня, является наличие поперечных импульсов у родительских пионов.
Предполагая, что пионы появляются в результате распада кластера, и считая
, что распад происходит изотропно при температуре ![]() , как
это предсказывается теорией и подтверждается экспериментально
(см., например,[2]), найдем угловую ширину конуса, в котором будут
испускаться пионы. В системе покоя кластера средний импульс частиц в
единицах
, как
это предсказывается теорией и подтверждается экспериментально
(см., например,[2]), найдем угловую ширину конуса, в котором будут
испускаться пионы. В системе покоя кластера средний импульс частиц в
единицах ![]() равен
равен
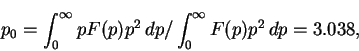 |
(33) |
| (34) |
Полагая, что кластер движется с лоренц-фактором ![]() и испускает
пион, который отклоняется от направления движения на угол
и испускает
пион, который отклоняется от направления движения на угол ![]() ,
получим для импульса в лабораторной системе с помощью преобразований
Лоренца:
,
получим для импульса в лабораторной системе с помощью преобразований
Лоренца:
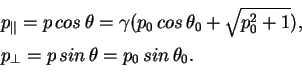 |
(35) |
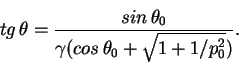 |
(36) |
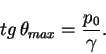 |
(37) |
Величина ![]() определяется как отношение
определяется как отношение
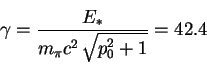 |
(38) |
| (39) |
Так как на меньших расстояниях от оси ![]() будут давать вклад пионы с
меньших высот, то функция пространственного распределения мюонов
будут давать вклад пионы с
меньших высот, то функция пространственного распределения мюонов ![]() должна возрастать с приближением к оси ливня. Если распределение генерации
пионов по высоте было бы однородным, то мы имели бы
должна возрастать с приближением к оси ливня. Если распределение генерации
пионов по высоте было бы однородным, то мы имели бы
| (40) |
Если к электронам в ливне применить аналогичные рассуждения и учесть,
что величиной ![]() для них является критическая энергия
для них является критическая энергия ![]() ,
а угол
,
а угол ![]() , следовательно, как и для пионов можно положить равным
, следовательно, как и для пионов можно положить равным
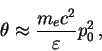 |
(41) |
Максимум электронного ливня достигается на глубине
![]() .
Это соответствует высоте
.
Это соответствует высоте ![]() =1.5 км. Характерный радиус ливня
=1.5 км. Характерный радиус ливня
| (42) |
Экспериментально наблюдаемые зависимости первичной энергии от числа
электронов и мюонов в ливне
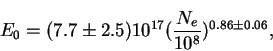 |
(43) |
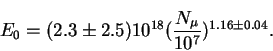 |
(44) |
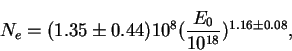 |
(45) |
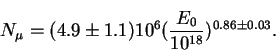 |
(46) |
Как видим, упрощенная теория дает близкие величины не только для показателей степени, но также и для амплитуд, то-есть, правильно (хотя и приближенно) предсказывает полное число частиц.
Приведенные здесь оценки для радиуса мюонов и электронов также неплохо согласуются с теоретическими и экспериментальными данными по функциям пространственного распределения.
Решающие доказательства того, что космические лучи являются заряженными частицами высоких энергий, были получены из широтных измерений. Геометрия магнитного поля Земли такова, что оно не допускает заряженные частицы извне в область экватора, поэтому измерения на низких широтах обнаруживают дефицит космических лучей по сравнению с высокоширотными измерениями.
Так как географические и геомагнитные полюса не совпадают, то тонкими измерениями удалось установить, что именно геомагнитное поле, а не другие возможные причины, ответственно за широтное распределение космических лучей.
Движение космических лучей в геомагнитном поле хорошо описывается теорией Штермера, созданной вначале для описания движения частиц, ответственных за полярные сияния. Здесь будет дано сильно упрощенное изложение этой теории.
Геомагнитное поле с хорошей точностью может быть описано полем диполя.
В сферической системе координат с полярной осью, проходящей через
геомагнитный полюс, поле имеет компоненты:
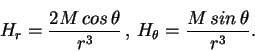 |
(47) |
Интегрируя дифферециальное уравнение
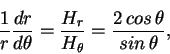 |
(48) |
| (49) |
Здесь ![]() - более привычная координата - геомагнитная широта.
- более привычная координата - геомагнитная широта.
Движение заряженной частицы определяется силой Лоренца
![\begin{displaymath}\vec F={e\over c}[\vec v\vec H].
\end{displaymath}](img105.gif) |
(50) |
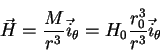 |
(51) |
Импульс частицы имеет ![]() -ю и
-ю и ![]() -ю компоненты.
-ю компоненты.
Поскольку частица совершает движение в одной плоскости, для его описания
можно использовать полярную систему координат, а вместо закона сохранения
количества движения удобнее всего воспользоваться законом сохранения
момента количества движения. Момент импульса ![]() изменяется
под действием момента силы
изменяется
под действием момента силы ![]() :
:
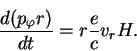 |
(52) |
Переходя к пространственной переменной ![]() в левой части равенства
посредством замены
в левой части равенства
посредством замены
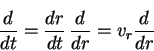 |
(53) |
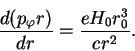 |
(54) |
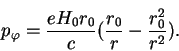 |
(55) |
Мы видим, что ![]() обращается в нуль при
обращается в нуль при ![]() и
стремится к нулю с ростом
и
стремится к нулю с ростом ![]() , а, следовательно, достигает максимальной
велечины при некотором промежуточном значении
, а, следовательно, достигает максимальной
велечины при некотором промежуточном значении ![]() . Приравнивая
нулю производную по
. Приравнивая
нулю производную по ![]() , находим, что
, находим, что ![]() .
.
Отсюда имеем
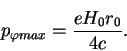 |
(56) |
Естественно, до точки ![]() дойдут лишь те частицы, у которых импульс
дойдут лишь те частицы, у которых импульс
![]() .
Следовательно, имеем пороговое значение импульса
.
Следовательно, имеем пороговое значение импульса
 |
(57) |
Подставляя приведенные выше значения в единицах ![]() для
для ![]() и
и
![]() , получим для порогового импульса
, получим для порогового импульса ![]() ГэВ/с (то-есть,
1.5 10
ГэВ/с (то-есть,
1.5 10![]() эВ/с).
эВ/с).
Для того, чтобы частица могла попасть на поверхность Земли на более
высокой широте, ей достаточно иметь импульс, превышающий порог для
данной широты, который меньше, чем на экваторе.
Широтную зависимость порога легко определить, сообразив, что для попадания
на широту ![]() частица должна достигнуть вершины силовой линии,
пересекающей земную поверхность на этой широте. Если, двигаясь вблизи
экваториальной плоскости, частица достигает
частица должна достигнуть вершины силовой линии,
пересекающей земную поверхность на этой широте. Если, двигаясь вблизи
экваториальной плоскости, частица достигает
![]() , то далее она вдоль силовой линии способна попасть
на поверхность Земли на широте
, то далее она вдоль силовой линии способна попасть
на поверхность Земли на широте ![]() .
.
Поле на расстоянии
![]() вблизи экватора равно
вблизи экватора равно
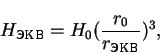 |
(58) |
| (59) |
Космическая среда пронизана слабыми, но протяженными магнитными полями. В результе действия силы Лоренца траектории частиц космических лучей являются искривленными, что критически влияет на судьбу частиц как в тех областях, где космические лучи возникают, так и там, где они распространяются. Рассмотрим последовательно однородное, слабо неоднородное и сильно неоднородное магнитное поле.
В однородном магнитном поле частицы космических лучей движутся по
винтовой линии, радиус которой определяется силой Лоренца
![\begin{displaymath}\vec F={e\over c}[\vec v\vec H].
\end{displaymath}](img105.gif) |
(60) |
Радиус, который называют ларморовым или гирорадиусом, равен
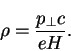 |
(61) |
Радиус зависит от поперечной к магнитному полю составляющей импульса, а не от полного импульса, что очевидным образом вытекает из выражения для силы Лоренца.
В слабо неоднородном или слабо переменном магнитном поле у частиц сохраняются, так называемые, инварианты.
Рассмотрим первый адиабатический инвариант. Его природа наиболее отчетливо видна для однородного поля, напряженность которого медленно меняется. Для простоты будем предполагать, что частица движется строго поперек поля и не будем специально оговаривать, что мы имеем дело с поперечным импульсом частиц.
Так как при изменении магнитного поля существует вихревое электрическое
поле, частица за один ларморовский оборот приобретает или теряет энергию
в соответствии с формулой
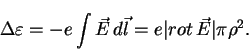 |
(62) |
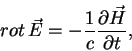 |
(63) |
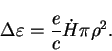 |
(64) |
Изменение импульса легко подсчитать, используя инвариант
![]() , откуда
, откуда
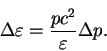 |
(65) |
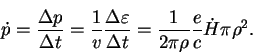 |
(66) |
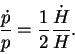 |
(67) |
Первый адиабатический инвариант, который мы получили, в случае
постоянного, но слабо неоднородного поля может быть записан
в разных формах:
| (68) |
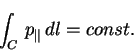 |
(69) |
Справедливость этого инварианта легко проверить, если заменить пробки
параллельными зеркалами. Пусть зеркала сближаются со скоростью ![]() ,
причем одно из них примем за неподвижное. При каждом соударении с
подвижным зеркалом подольный импульс (перпендикулярный к поверхности
зеркал) получает приращение
,
причем одно из них примем за неподвижное. При каждом соударении с
подвижным зеркалом подольный импульс (перпендикулярный к поверхности
зеркал) получает приращение
![]() . Время между
такими соударениями составляет
. Время между
такими соударениями составляет ![]() , где
, где ![]() - расстояние
между зеркалами. Средняя скорость изменения импульса
- расстояние
между зеркалами. Средняя скорость изменения импульса
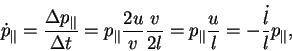 |
(70) |
Рассмотрим ловушку, которая меняет свой объем, сохраняя подобие размеров,
то-есть, при неизменной форме. Пусть каждый размер увеличился в ![]() раз.
Тогда поперечный импульс уменьшится в
раз.
Тогда поперечный импульс уменьшится в ![]() раз, поскольку
раз, поскольку ![]() .
Во столько же раз уменьшится и продольный импульс. Можем записать
поэтому еще один инвариант
.
Во столько же раз уменьшится и продольный импульс. Можем записать
поэтому еще один инвариант
| (71) |
В случае сильно неоднородного поля, когда оно значительно изменяется на длине гирорадиуса, движение частицы уподобляется хаотическому блужданию и допускает лишь статистическое описание с помощью функции распределения.
Космические лучи представляют собой релятивистский газ и их полное
описание требует знания функции времени и 6 пространственных и
импульсных переменных, образующих фазовое пространство:
![]() . В отличие от обычного газа, где
. В отличие от обычного газа, где
![]() и фазовое пространство часто строят на переменных
и фазовое пространство часто строят на переменных
![]() , здесь использование переменной
, здесь использование переменной ![]() было бы
крайне неудобным, так как
было бы
крайне неудобным, так как ![]() , и необходимо использовать импульс.
Так как в большинстве случаев распределение космических лучей очень
близко к изотропии, функция распределения
, и необходимо использовать импульс.
Так как в большинстве случаев распределение космических лучей очень
близко к изотропии, функция распределения ![]() может
быть заменена плотностью
может
быть заменена плотностью ![]() , в которой охватываются
все частицы, имеющие одинаковый модуль импульса. Если функция
, в которой охватываются
все частицы, имеющие одинаковый модуль импульса. Если функция ![]() отражает число частиц в элементе импульсного пространства
отражает число частиц в элементе импульсного пространства
![]() , то плотность
, то плотность ![]() относится ко всем частицам,
импульс которых по модулю попадает в интервал
относится ко всем частицам,
импульс которых по модулю попадает в интервал ![]() . Поэтому существует
связь:
. Поэтому существует
связь:
| (72) |
В мелкомасштабных неоднородных магнитных полях траектории частиц сильно запутываются и можно в первом приближении считать, что частицы заключены в некотором объеме, который может рассматриваться как ловушка. При изменении этого объема плотность частиц будет меняться.
Пусть ![]() частиц заключены в объеме
частиц заключены в объеме ![]() , так что плотность
, так что плотность ![]() .
Изменение плотности
.
Изменение плотности
 |
(73) |
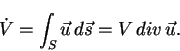 |
(74) |
Следовательно, имеем изменение плотности в объеме
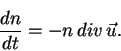 |
(75) |
Обычно интересуются изменением какой-либо величины в заданной точке
пространства. Если величина имеет градиент и среда движется, то в
заданной точке будет наблюдаться изменение, которое в нашам случае имеет
вид:
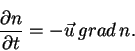 |
(76) |
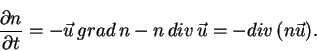 |
(77) |
Уравнение носит название уравнения непрерывности и хорошо известно. Вывод его здесь сделан для того, чтобы можно было лучше разобраться в последующих модификациях этого уравнения.
Так как объем, в котором заключены частицы, может рассматриваться
как ловушка, то при изменении объема будет меняться и импульс частиц.
Дифференцируя по времени инвариант, связывающий импульс частиц и занимаемый
ими объем, получим
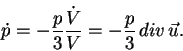 |
(78) |
Переменные, от которых зависит плотность, - три пространственные
координаты и модуль импульса - можно рассматривать как четырехмерное
пространство, в котором скорость перемещения частиц по четвертой
координате равна ![]() . Обобщая обычное уравнение непрерывности
на случай 4 переменных, получаем уравнение
. Обобщая обычное уравнение непрерывности
на случай 4 переменных, получаем уравнение
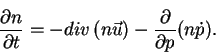 |
(79) |
Теперь необходимо обратить внимание на то, что ловушка не является
идеальной и частицы способны просачиваться из области, где их много, туда,
где их мало. Поэтому обычный перенос частиц с веществом ![]() следует дополнить членом, пропорциональным градиенту плотности:
следует дополнить членом, пропорциональным градиенту плотности:
![]() . Коэффициент
. Коэффициент ![]() характеризует скорость просачивания и носит название коэффициента диффузии.
Подставляя это выражение, а также выражение для
характеризует скорость просачивания и носит название коэффициента диффузии.
Подставляя это выражение, а также выражение для ![]() в уравнение,
получаем уравнение переноса космических лучей:
в уравнение,
получаем уравнение переноса космических лучей:
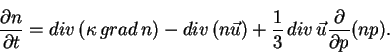 |
(80) |
Это уравнение описывает перенос, а также замедление или ускорение частиц в различных космических условиях.
Уравнение переноса часто записывают для функции распределения
![]() . Выразим
. Выразим ![]() через
через ![]() и произведем дифференцирование
по частям во втором и третьем членах правой части. Члены вида
и произведем дифференцирование
по частям во втором и третьем членах правой части. Члены вида
![]() взаимно уничтожатся и мы получим
взаимно уничтожатся и мы получим
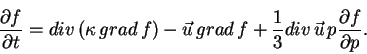 |
(81) |
Ускорение космических лучей ударными волнами - сложный процесс,
в котором ускоряемые частицы получают настолько большую долю энергии,
несомой волной, что оказывают обратное воздействие на структуру
волны - как на поле скоростей среды, так и на магнитное поле.
Если пренебречь обратным воздействием и рассматривать ускорение пробных
частиц в заданных условиях, то наиболее прстое описание получим для ударной
волны с бесконечно тонким фронтом, у которой скорость газа в системе,
где фронт покоится,
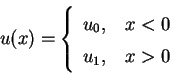 |
(82) |
В уравнение переноса
 |
(83) |
Получим сначала решение однородного уравнения. Так как
![]() - всюду равно нулю, кроме точки
- всюду равно нулю, кроме точки ![]() ,
то получим решение отдельно для левого и правого полупространства.
,
то получим решение отдельно для левого и правого полупространства.
Имеем после однократного интегрирования по ![]() :
:
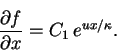 |
(84) |
Для правого полупространства ![]() , поскольку растущего решения там
быть не может, и следующее интегрирование по
, поскольку растущего решения там
быть не может, и следующее интегрирование по ![]() дает
дает
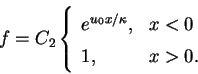 |
(85) |
Так как функция ![]() в точке
в точке ![]() имеет излом, то ее первая производная
терпит разрыв, а вторая производная обращается здесь в бесконечность
и бесконечные члены должны взаимно погашаться:
имеет излом, то ее первая производная
терпит разрыв, а вторая производная обращается здесь в бесконечность
и бесконечные члены должны взаимно погашаться:
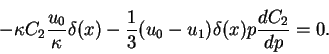 |
(86) |
Напомним, что мы решаем однородное уравнение и источник пока не принимаем во внимание.
Постоянная интегрирования, как мы видим, должна зависеть от ![]() степенным образом:
степенным образом:
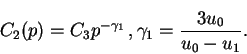 |
(87) |
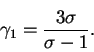 |
(88) |
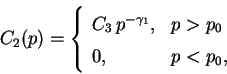 |
(89) |
Следовательно,
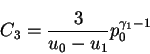 |
(90) |
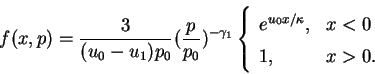 |
(91) |
Подчеркнем, что здесь коэффициент диффузии ![]() может каким угодно
образом зависеть от
может каким угодно
образом зависеть от ![]() .
.
Как видно из этого решения, функция распределения является степенной функцией импульса, показатель которой зависит только от степени сжатия ударной волны. Эта последняя величина для сильных ударных волн лежит в узких пределах, что делает степенной спектр частиц весьма устойчивым к изменяющимся конкретным условиям.
Рассмотрим более детально, что происходит с частицей, когда она пересекает
ударный фронт. Когда частица влетает в левое полупространство, где
среда движется ей навстречу со скоростью ![]() , то она прибретает
дополнительную энергию за счет встречного соударения. Хотя частица
может рассеиваться много раз, она с вероятностью единица пересечет фронт в
обратном напрвлении. Для того, чтобы рассчитать, какое среднее приращение
получит импульс частицы за период между двумя пересечениями фронта,
можно этот процесс рассматривать как отражение от движущегося зеркала.
, то она прибретает
дополнительную энергию за счет встречного соударения. Хотя частица
может рассеиваться много раз, она с вероятностью единица пересечет фронт в
обратном напрвлении. Для того, чтобы рассчитать, какое среднее приращение
получит импульс частицы за период между двумя пересечениями фронта,
можно этот процесс рассматривать как отражение от движущегося зеркала.
Если частица падает на зеркало перпендикулярно к его поверхности, то
после отражения ее импульс ![]() возратет на
возратет на
![]() ,
где
,
где ![]() - скорость частицы. При скользящем падении под углом
- скорость частицы. При скользящем падении под углом ![]() к нормали приращение получит только нормальная составляющая импульса
и оно составит
к нормали приращение получит только нормальная составляющая импульса
и оно составит
![]() . Число частиц,
падающих в единицу времени на единичную площадку зеркала в интервале
углов
. Число частиц,
падающих в единицу времени на единичную площадку зеркала в интервале
углов
![]() равно
равно
![]() . Полное число частиц, падающих под
углами
. Полное число частиц, падающих под
углами
![]() , составит
, составит ![]() , а суммарный импульс,
полученный ими, будет равен
, а суммарный импульс,
полученный ими, будет равен ![]() . Эта последняя величина
получена умножением приращения импульса на число частиц ипоследующим
интегрированием по всем углам. Следовательно, среднее приащение
импульса у одной частицы составит
. Эта последняя величина
получена умножением приращения импульса на число частиц ипоследующим
интегрированием по всем углам. Следовательно, среднее приащение
импульса у одной частицы составит ![]() .
.
В правом же полупространстве между двумя пересечениями фронта частица
будет терять импульс: ![]() . За весь цикл, когда
частица пересекает фронт в одном и том же направлении, среднее
приобретение импульса составит
. За весь цикл, когда
частица пересекает фронт в одном и том же направлении, среднее
приобретение импульса составит
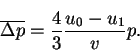 |
(92) |
В правом полупространстве частица имеет вероятность не вернуться к фронту,
так как рассеивающая среда удаляется от него со скоростью ![]() .
Среда через каждую единичную площадку уносит
.
Среда через каждую единичную площадку уносит ![]() частиц. Так как
на фронт падает в единицу времени
частиц. Так как
на фронт падает в единицу времени ![]() частиц и эта величина много больше,
чем
частиц и эта величина много больше,
чем ![]() , то вероятность того, что частица не вернется к фронту,
много меньше единицы. В этом главная причина эффективности рассматриваемого
механизма ускорения. Вероятность потери частицы
, то вероятность того, что частица не вернется к фронту,
много меньше единицы. В этом главная причина эффективности рассматриваемого
механизма ускорения. Вероятность потери частицы ![]() равна отношению
указанных потоков:
равна отношению
указанных потоков:
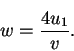 |
(93) |
Если проследить за судьбой частицы, испытавшей ![]() полных циклов пересечения
фронта, то для импульса этих частиц можно записать
полных циклов пересечения
фронта, то для импульса этих частиц можно записать
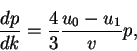 |
(94) |
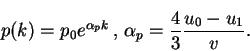 |
(95) |
А для числа частиц имеем
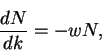 |
(96) |
| (97) |
Если заменить теперь величину ![]() ее выражением через импульс
ее выражением через импульс
![]() , то получим
, то получим
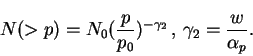 |
(98) |
Мы получили интегральный степенной спектр с показателем
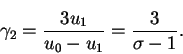 |
(99) |
Дифференциальный спектр для плотности частиц также будет степенным,
но величина показателя будет на единицу больше:
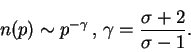 |
(100) |
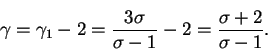 |
(101) |
Таким образом, детальное кинетическое рассмотрение процесса и решение уравнения переноса дают совпадающие результаты.